Introduzione
Questo articolo si concentra su un tema chiave dei Large Language Models (LLM, modelli linguistici di grandi dimensioni): gli embeddings. In particolare, esploriamo il modo in cui i LLM trasformano e rappresentano le parole, nonché l’approccio matematico utilizzato per stimare le somiglianze attraverso la funzione coseno di similitudine (cosine similarity).
Possiamo pensare a un embedding come a una sorta di “impronta digitale del significato” di un testo o di un concetto. Pertanto gli embeddings hanno un ruolo fondamentale per confrontare significati, trovare testi correlati, cercare documenti, raggruppare argomenti e molto altro, attività che sarebbero probabilmente impossibili con rappresentazioni testuali.
Nel prossimo articolo, l’attenzione si sposterà sul funzionamento complessivo degli LLM, in cui verranno integrati tutti i vari componenti e ogni parte del mosaico verrà posizionato al proprio posto creando un chiaro quadro d’insieme.
Embeddings aka Vectors
I modelli LLM devono memorizzare informazioni sugli elementi del mondo reale e sui concetti astratti. Per raggiungere questo obiettivo, gestiscono le informazioni utilizzando array di numeri noti come embeddings o vettori: in pratica, si tratta di un termine relativamente nuovo per indicare il vecchio concetto di lista strutturata di elementi.
Questi vettori vengono comunemente utilizzati per rappresentare punti in uno spazio multidimensionale. Ciascun elemento di un vettore corrisponde a una specifica dimensione, e la combinazione di questi elementi definisce la posizione del vettore in tale spazio. Gli embeddings sono fondamentali per misurare le somiglianze e trasformare i dati.
Sebbene per noi esseri umani possa risultare difficile visualizzare anche uno spazio tridimensionale, il software non ha questa limitazione. Ad esempio, ChatGPT-3 gestisce vettori di parole di dimensioni pari a 12.288 [Timothy e Trott, 2023b], mentre si ritiene che ChatGPT-4 utilizzi vettori di parole di dimensioni pari a 16.000 elementi; questa dimensione deve essere considerata indicativa, poiché è stata menzionata da diversi articoli commerciali, ma non è mai stata ufficialmente confermata.
Utilizzare una rappresentazione puramente testuale (formato stringa) non consentirebbe ai LLM di fare le operazioni complesse di cui sono capaci.
Come discusso nel primo articolo, una rete neurale viene addestrata affinché testi con significati simili producano vettori simili. Questo addestramento utilizza, tipicamente, immense fonti testuali che fanno sì che elementi correlati tendano a collocarsi vicini nello spazio vettoriale.
Pensiamo a un embedding come una specie di “impronta digitale del significato” di un testo o di un’entità, o come un “segnaposto” di significato: così come le coordinate individuano un luogo su una mappa, un embedding individua un significato in uno spazio semantico. “Un embedding è una rappresentazione appresa del testo, in cui le parole che hanno lo stesso significato possiedono una rappresentazione simile” [Tomas Mikolov et al., 2013].
Un esempio con le auto
Consideriamo ora un semplice esempio basato sulle automobili. Il modello linguistico potrebbe creare un embedding a 4 dimensioni con i seguenti attributi:
- abilità su strada
- abilità fuoristrada
- capacità passeggeri
- abilità in acqua
Ora prendiamo in considerazione i seguenti veicoli: un’auto familiare, un SUV, un’auto di Formula 1, un’auto da rally e un vero e proprio fuoristrada. Sebbene queste categorie siano ancora piuttosto generiche — ad esempio, la categoria SUV include svariati modelli con caratteristiche molto differenti — tale semplificazione è sufficiente per gli scopi dell’esempio.
A questo punto, possiamo assegnare i valori come riassunto nella tabella 1.
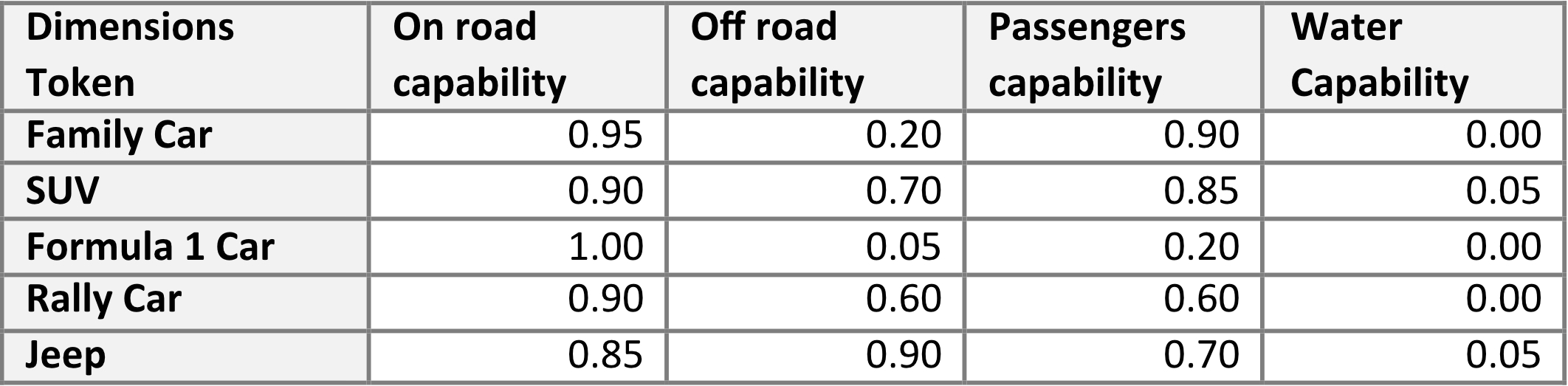
Da una prima e superficiale analisi delle varie valutazioni, è già possibile trarre alcune conclusioni iniziali. Ad esempio, le auto SUV e le Jeep risultano molto simili, mentre una vettura di Formula 1 e una Jeep sono piuttosto dissimili. Tuttavia, i modelli necessitano di un approccio scientifico/matematico per poter confrontare gli elementi e trarre conclusioni. Ciò richiede ulteriori passaggi, come descritto nel paragrafo seguente.
Un esempio con entità che volano
Seguendo l’esempio proposto da Guillaume Desagulier [Desagulier, 2018], supponiamo che esista una funzione che, data una parola, sia in grado di restituirne la rappresentazione in base ai seguenti tre fattori:
- ali
- motore
- cielo
Consideriamo le seguenti parole:
- ape
- aquila
- oca
- elicottero
- drone
- razzo
- jet
Nella terminologia degli LLM, queste parole sono definite come token.
Ora, immaginiamo di sottoporre questi token a una funzione che restituisca la loro rappresentazione in termini dei tre contesti (ali, motore e cielo). Questo processo ci consente di creare la tabella 2.
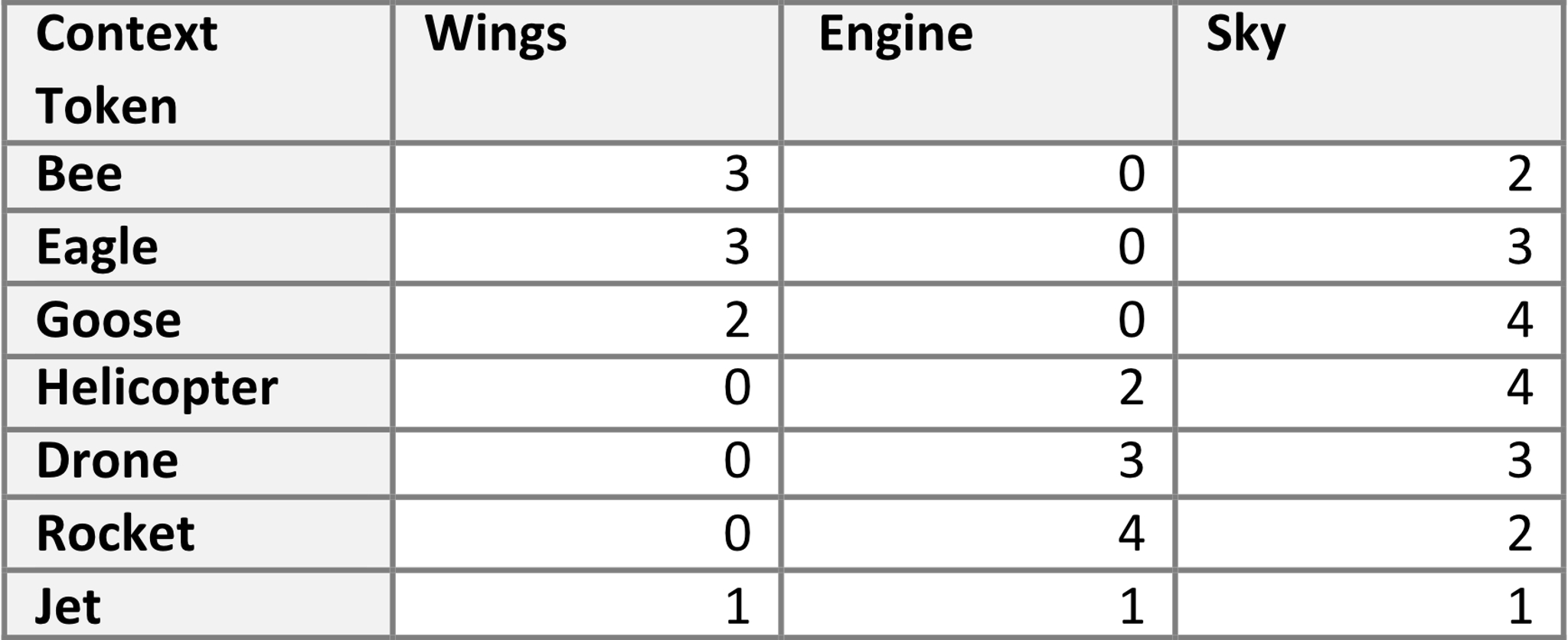
Ogni parola occupa una posizione specifica nello spazio vettoriale. Secondo questo modello ipotetico, le coordinate per l’insetto ape potrebbero essere (3, 0, 2), mentre il velivolo elicottero potrebbe essere rappresentato dalle coordinate (0, 2, 4). Ciò ci consente di visualizzare queste parole in uno spazio tridimensionale (figura 1). Sebbene in questo esempio abbiamo scelto tre contesti, negli scenari reali — come discusso in precedenza — la matrice in un LLM comprende facilmente migliaia di dimensioni.
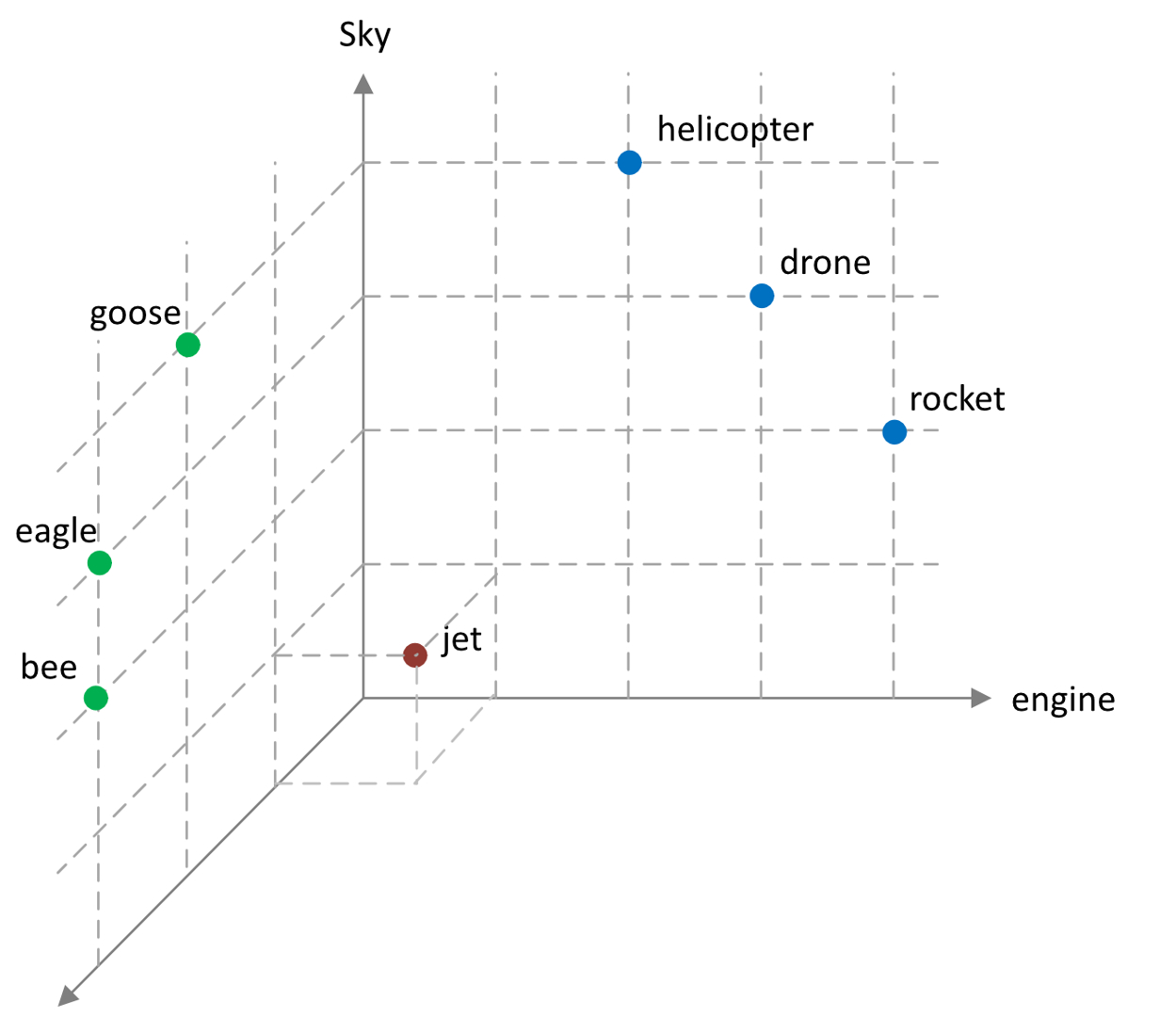
Stesso esempio, diversa rappresentazione
Inoltre, è possibile rappresentare esplicitamente i sette vettori come frecce che originano dal punto in cui i tre assi si intersecano, estendendosi fino ai rispettivi punti finali definiti dalle loro coordinate (figura 2).
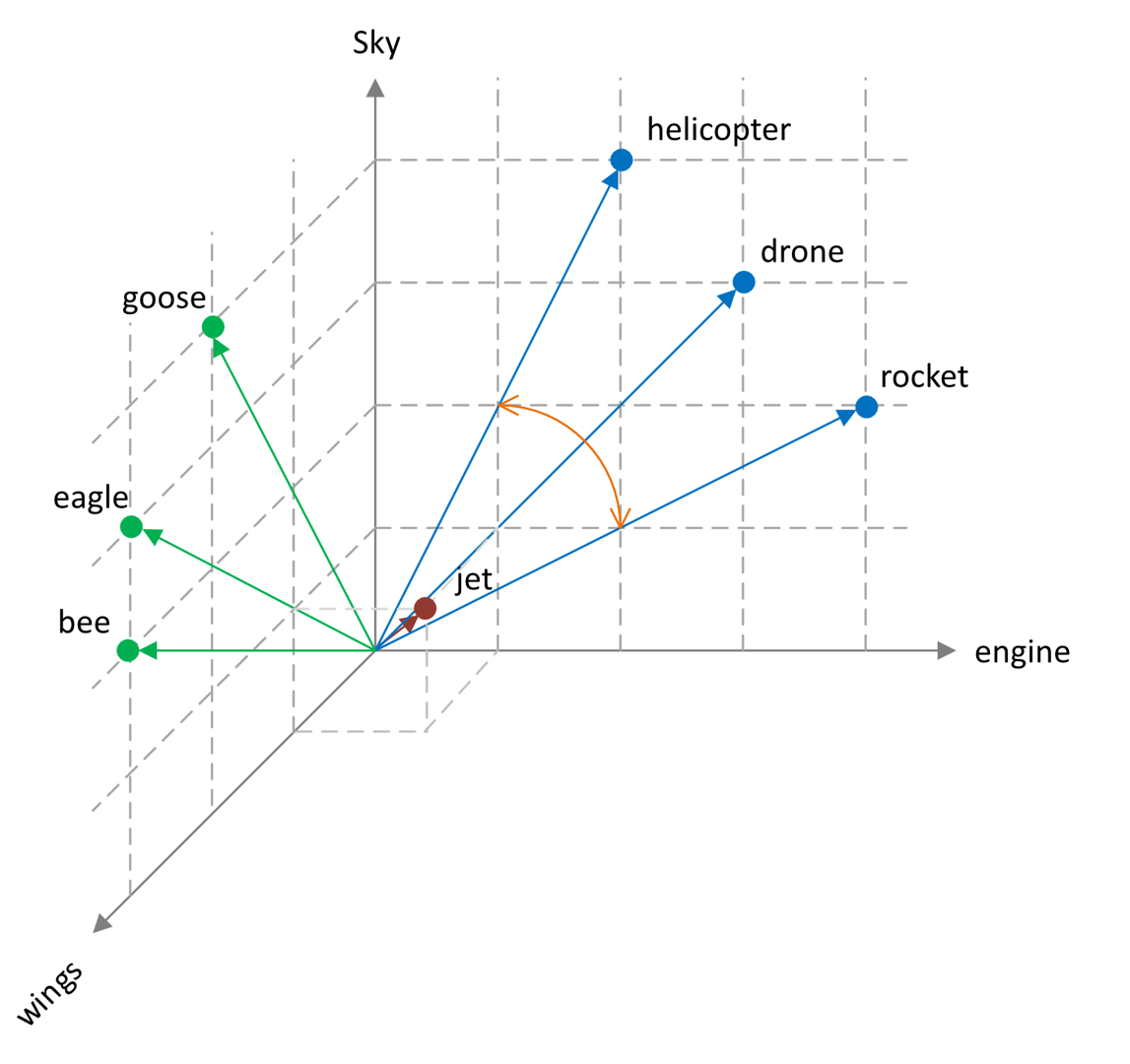
Una volta stabiliti i vettori, possiamo calcolare la distanza o la somiglianza tra di essi.
Cosine similarity
Un metodo comune per calcolare distanza o somiglianza tra i vettori è la funzione di Cosine Similarity (coseno di somiglianza). Questa funzione restituisce un valore compreso in un intervallo limitato tra –1 e 1. Un valore vicino a 0 indica che i due vettori sono ortogonali (perpendicolari) tra loro, suggerendo bassa o nessuna somiglianza. Al contrario, un valore vicino a 1 indica che l’angolo tra i vettori è piccolo, segnalando un grado di somiglianza elevato, fino al valore 1 in cui è massimo.
Ad esempio, la somiglianza del coseno tra i vettori che rappresentano “elicottero” e “razzo” è pari a 0,80, suggerendo un livello di somiglianza relativamente alto. Per finire, un valore di –1 indica che i vettori sono diametralmente opposti, puntando in direzioni opposte. Nel nostro esempio, la funzione coseno di similarità genererebbe solo valori nell’insieme (0, 1), perché gli elementi presi in considerazione hanno almeno una qualche similarità: volano.
Applicando la funzione di cosine similarity a tutte le coppie di parole, è possibile generare la seguente matrice (vedi Tabella 3):
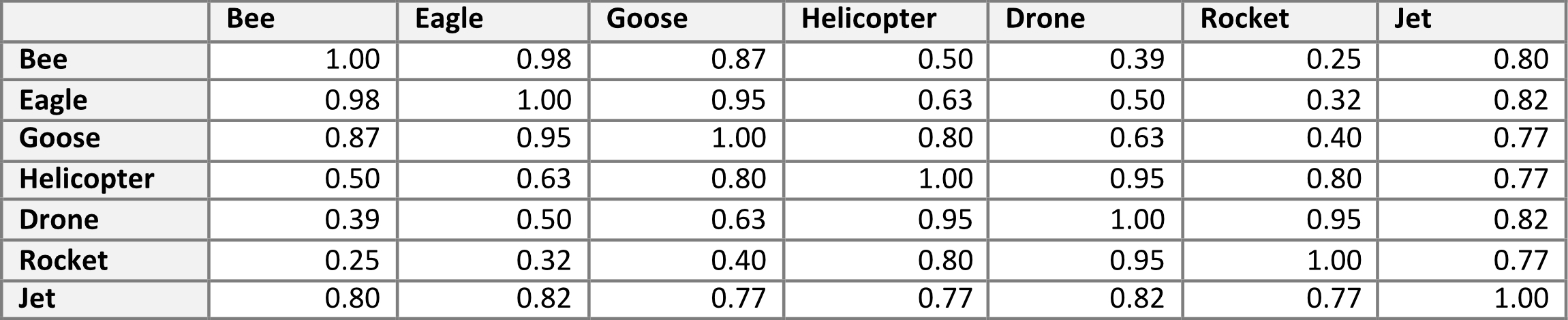
L’esempio descritto finora è semplice, ma dovrebbe fornire ai lettori una comprensione di base del tipo di rappresentazioni interne che il modello può utilizzare.
Un terzo esempio: le città
Numerosi articoli [Timothy e Trott, 2023a] e libri forniscono esempi basati sulle città. Ad esempio, potremmo considerare le seguenti città insieme alle loro coordinate geografiche:
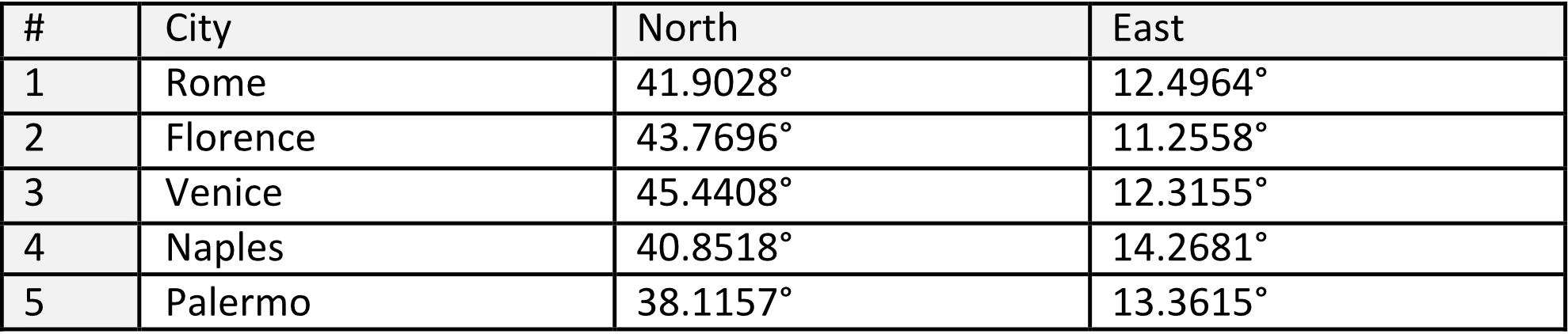
Possiamo definire la distanza tra le città come la distanza in linea d’aria. Ad esempio, la distanza da Roma a Firenze è di 274,95 km, e da Roma a Venezia è di 529,63 km, e così via. Di conseguenza, possiamo affermare che Napoli è vicina a Palermo — in linea d’aria ovviamente — e Roma è vicina a Napoli. Al contrario, Venezia è lontana da Palermo. Se registrassimo le distanze di ciascuna città rispetto a tutte le altre, creeremmo una rappresentazione numerica di quella città in uno spazio multidimensionale, simile a quanto mostrato nella Tabella 2.
Allo stesso modo, nei modelli linguistici, ogni parola (o token) è rappresentata da un vettore in uno spazio ad alta dimensionalità. Le parole con significati simili si trovano vicine tra loro, proprio come le città vicine nello spazio geografico. Ad esempio, parole vicine a “Ferrari” potrebbero includere “auto”, “F1”, “rosso”, “potenza”, “bolide”, “Enzo” e così via.
Aspetti matematici del coseno di somiglianza
Questo paragrafo non è fondamentale per la comprensione del presente articolo, tuttavia offre approfondimenti per chi è interessato ad alcuni aspetti tecnici [Singhal, 2001].
La cosine similarity è uno strumento potente per misurare quanto due “entità” — o, più precisamente, le loro rappresentazioni vettoriali — siano simili. Funziona calcolando l’angolo tra i vettori:
- un valore pari a 1 indica che i vettori hanno la stessa direzione;
- un valore pari a 0 indica che sono ortogonali (non correlati);
- un valore pari a –1 indica che sono opposti.
Il calcolo in sé è piuttosto semplice, aspetto non secondario per sistemi di grandi dimensioni: consiste nel prodotto scalare dei due vettori diviso per il prodotto delle loro magnitudini. Questo metodo, semplice ma efficace, è ampiamente utilizzato in applicazioni come motori di ricerca, sistemi di raccomandazione e natural language processing per identificare relazioni e schemi nei dati. La formula è:
Dove:
- A⋅B prodotto scalare dei due vettori;
- ∥A∥ e ∥B∥ prodotto delle “lunghezze”, magnitudini, dei due vettori.
Si considerino i seguenti due vettori a solo due dimensioni:
- A=[1,2]
- B=[2,3]
Si avrà quindi che il prodotto scalare sarà
A⋅B=(1×2)+(2×3)=2+6=8
La magnitudini daranno
∥A∥=12+22=5 ∥B∥=22+32=13
E quindi il coseno di similarità sarà
Cosine similarity=5×138≈8.068≈0.99
Il risultato generato dal calcolo è 0.99. Ciò significa che i due vettori, e quindi le entità che essi rappresentano, sono molto simili.
Embedding nel contesto dei modelli LLM
Nel prossimo articolo approfondiremo i meccanismi di alto livello dei modelli LLM, fornendo una visione chiara e strutturata del loro funzionamento. Possiamo immaginarlo come l’assemblaggio finale di una macchina di precisione, in cui ogni ingranaggio verrà incastrato nel proprio posto per far funzionare l’intero sistema.
Prima di concludere questo articolo però, prepariamo il terreno per comprendere gli embeddings nel giusto contesto attraverso un altro semplice esempio.
Immaginiamo che un utente richieda il seguente prompt (piuttosto generico!):
“Summarise the main points of AI.”
(“Riassumi i punti principali dell’intelligenza artificiale.”)
Tokenizer
Il primo passo del processo è la tokenizzazione, un componente fondamentale del funzionamento degli LLM. La “tokenizzazione” suddivide il testo in unità più piccole e gestibili chiamate token, che il modello può elaborare. Questi token possono rappresentare parole, sotto-parole o persino singoli caratteri, a seconda del tipo di tokenizer utilizzato.
Per il prompt
“Summarise the main points of AI.”
utilizzando un tokenizer basato su sotto-parole, come Byte Pair Encoding o WordPiece, comunemente utilizzati dai modelli come GPT, lo strumento potrebbe suddividerlo in token come segue:
[“Summarise”, “the”, “main”, “points”, “of”, “AI”]
Se si applicasse la tokenizzazione a livello di sotto-parole, potrebbe generare la seguente suddivisione:
[“Summ”, “arise”, “the”, “main”, “points”, “of”, “AI”]
Il termine “Summarise” potrebbe essere suddiviso in due sotto-parole per catturare somiglianze con verbi come “Sum up”, e così via.
Generazione degli Embedding
Ogni token viene quindi associato a un ID univoco attingendo al vocabolario del modello. Una volta ottenuti i token dalle parole, essi vengono convertiti in una rappresentazione numerica vettoriale (embedding). Questi embeddings sono vettori ad alta dimensionalità che catturano il significato semantico dei token.
Token Id: ogni token è mappato a un ID univoco nel vocabolario del modello. Ad esempio:
[“Summarise”, “the”, “main”, “points”, “of”, “AI”] [1234, 56, 789, 1011, 23, 4567]
Questi numeri sono solo esempi casuali; gli ID reali dipendono dal vocabolario del modello.
Embedding Lookup: gli ID dei token vengono poi utilizzati per recuperare i corrispondenti embeddings da una matrice di embeddings pre-addestrata. Ogni ID di token corrisponde a un vettore di dimensione fissa: in GPT-3 ci sono 768 dimensioni. Esempio:
1234 → [0.12, -0.34, 0.56, ..., 0.78] 56 → [0.01, 0.45, -0.67, ..., 0.89]
Positional Encoding: Per tenere conto dell’ordine dei token nella sequenza, vengono aggiunti positional encodings agli embeddings. Ciò garantisce che il modello comprenda la struttura della sequenza. Ad esempio, “AI of points main the Summarise” avrebbe un significato completamente diverso.
Output finale
Il risultato finale è una sequenza di embeddings, uno per ciascun token, che viene poi passata al modello di intelligenza artificiale per ulteriori elaborazioni.
Ad esempio:
- [0.12, -0.34, 0.56, …, 0.78] → “Summarise”
- [0.01, 0.45, -0.67, …, 0.89] → “the”
- [0.23, -0.12, 0.34, …, 0.56] → “main”
- …
Da notare che alcuni tokenizer ignorano gli articoli e altre particelle grammaticali simili, in quanto non contribuiscono al valore semantico della frase.
Questi embeddings vengono quindi utilizzati dai livelli della rete neurale del modello per eseguire operazioni come comprendere, riassumere o generare testo.
Conclusioni
I modelli LLM rappresentano le parole come vettori n-dimensionali chiamati “ embeddings”. Questi embeddings catturano le relazioni semantiche tra le parole, permettendo ai computer di elaborare e analizzare i linguaggi, naturali e non, in modo numerico. La funzione matematica che converte il testo in questi vettori numerici consente ai modelli LLM di comprendere semanticamente e quindi operare con il linguaggio umano.
Quando un utente fornisce un prompt al modello, un primo passo è la tokenizzazione. Questo processo si occupa di suddividere il testo in unità più piccole e digeribili chiamate token, che il modello può poi elaborare. A ciascun token viene assegnato un ID unico, attingendo dal vocabolario del modello, che poi è convertito in una rappresentazione numerica. Questi ID dei token vengono utilizzati per recuperare i loro corrispondenti embeddings da una matrice di embeddings preaddestrata, dove ciascun ID del token viene mappato su un vettore di dimensione fissa (p.e., dimensione pari a 768 per GPT-3). Per tenere conto dell’ordine dei token nella sequenza, vengono aggiunti agli embeddings degli encoding posizionali, garantendo che il modello comprenda la struttura secondo la sequenza originale. Il risultato è una sequenza di embeddings, uno per ciascun token, che viene poi passata al modello LLM per ulteriori elaborazioni.
Riferimenti
[Timothy and Trott, 2023a] Timothy B Lee – Sean Trott, Large language models, explained with a minimum of math and jargon. 27 july 2023,
https://www.understandingai.org/p/large-language-models-explained-with
[Timothy and Trott, 2023b] Timothy B Lee – Sean Trott, A jargon-free explanation of how AI large language models work. Ars Technica, 31 july 2023
https://arstechnica.com/science/2023/07/a-jargon-free-explanation-of-how-ai-large-language-models-work/8/
[Tomas Mikolov et al., 2013] Tomas Mikolov – Kai Chen, Greg Corrado – Jeffrey Dean, Efficient Estimation of Word Representations in Vector Space” (last revised 7 Sep 2013)
https://arxiv.org/abs/1301.3781
[Desagulier, 2018] Guillaume Desagulier, Word embeddings: the (very) basics. Hypothesis, 25/04/2018
https://corpling.hypotheses.org/495
[Singhal 2001] Singhal Amit, Modern Information Retrieval: A Brief Overview. Bulletin of the IEEE Computer Society Technical Committee on Data Engineering 24 (4): 35–43, 2001




